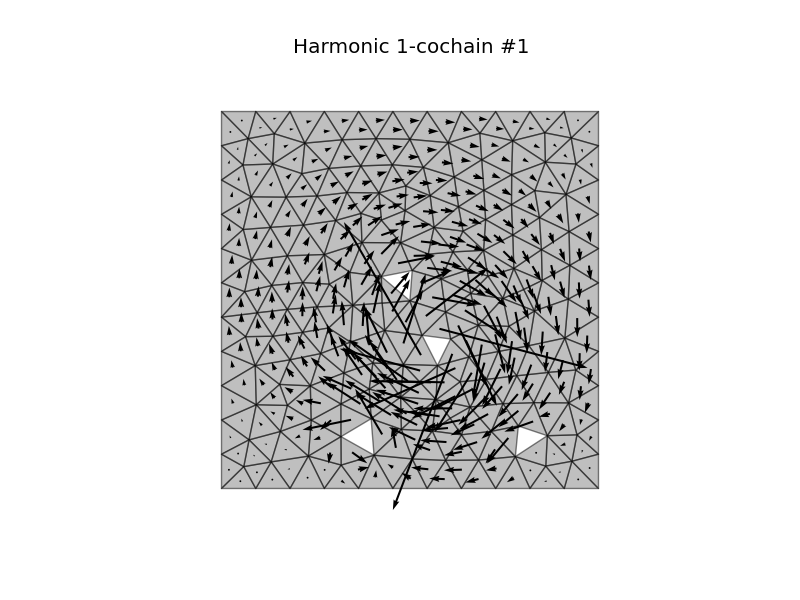
I’ll try to explain the idea in more detail: Possible use equations on simplicial meshes is developed based on discrete exterior calculus (DEC). It is use discretization on simplicial complexes such as triangle and tetrahedral meshes. Method is the use of an algebraic discretization of the contraction operator and a combinatorial discretization of the wedge product. Also develop a discretization for spatially dependent Hodge star that varies with the permeability of the medium. Equations of any physical process automatically are first rewritten using the exterior calculus notation. We change differential operators by the exterior derivative, Hodge star and wedge product operators. Discrete operators based on the python framework.
As a result, our calculations are reduced to the multiplication cycle of our data into two-three the matrices are calculated for each time point. Each element of the matrix connected to the finite element of the object (part of engine). The key point is that all steps are automated and the algorithm calculates and physical fields too.
The center of mass can be regarded as a dipole field. Enter additional space for this point of the center of mass. And to build additional space graph of incidence between the parts. Depending on the weight of the edges of the graph (in the topology and metric of the dual space) decisive influence or not parts of system.
An exemplary dual space of the landscape can be calculated in advance.