Geometric algebra, what is it? In the School, study Algebra and Geometry separately.
In Algebra, the numbers are replaced with letters in the very first step and an attempt is made to manipulate only the symbols. Typically, combinations of symbols and operations are made.
In the course of Stereometry solve problems associated with three-dimensional figures. Rarely, when the proofs or solutions of a problem are based on manipulating pieces of figure volumes.
In real life, for example, a carpenter, locksmith or any other craftsman operates only with three-dimensional things.
Is it possible to combine a symbolic record and manipulation with three-dimensional objects and objects of greater dimension?
Yes, it is possible.
William Kingdon Clifford created an Algebra that can manipulate multidimensional objects.
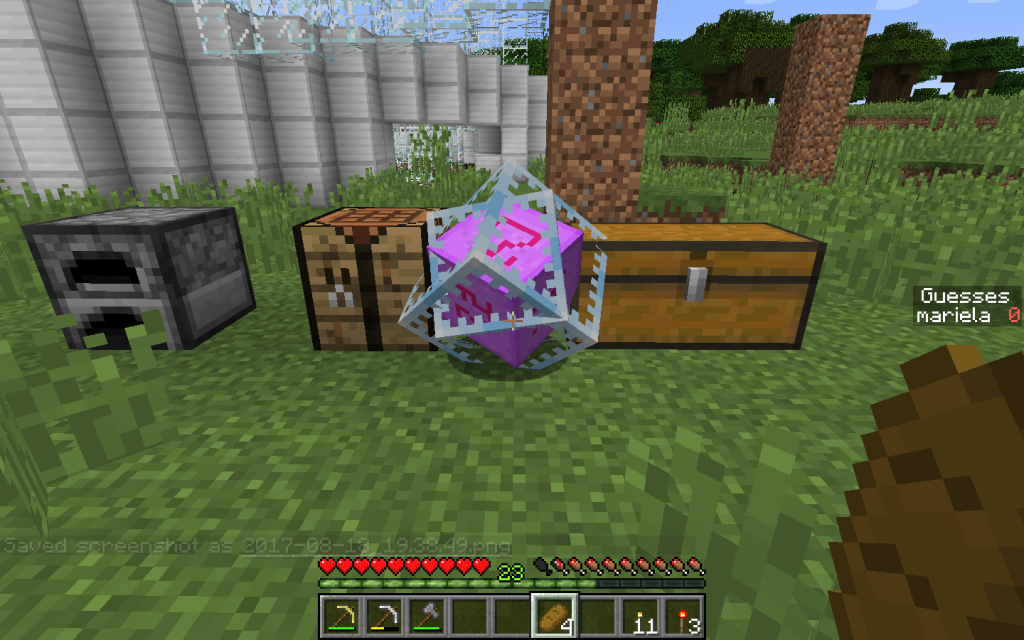
In order to better represent this algebra, let’s do spawn of Ender Crystal in Minecraft. This is a very fascinating adventure search for the fortress with a portal to the parallel world, killing the dragon and returning with ender_crystal. But we will shorten this long adventure in order to engage in Mathematics.
Note that inside the pink cube with Nepal ligatures there is a very powerful flywheel in the gyroscopic suspension and most likely not of a mechanical nature. Therefore, one blow is sufficient for any object on the ender_crystal to provoke a big explosion.
/jsp spawn ender_crystal
We consider the construction ender_crystal to be the basis of our Euclidean three-dimensional space.
Scalar
Then the vertex that is under the ground in the picture while moving ender_crystal down will be the Unit of our Algebra and the Scalar element. We denote it by unity (1).
Vector
The three Ribs of the outer cube emanating from this unit will be the Base Vectors. They are directed upwards from the Unit. They can also be called Oriented Linear Elements. We will consider them numbered from 1 to 3.
Usually this ends the study of the mathematical basis for Physics, but we will go further. We will add 2 more element types.
Bivector
Basic Bivector (pseudovector) are the faces of the outer cube that are formed by each pair of Basic Vectors. Oriented flat elements. When moving in the direction of the first vector from the pair in the plane of the face along the circle to the second basis vector, the direction of the plane element corresponds to the third orthogonal basis vector (it is not in the illustration, since it is directed perpendicular to the plane).
If we move in the opposite direction from the second base element to the first one, the direction of the oriented flat element will be opposite to the third basis vector.
Trivector
The third basic element is the volume. We call its basic trivector (or pseudoscalar). for it, rotation is also specified. If the unit is taken as the base of the axis of rotation of the inner frame cube (which passes through the top of the outer cube). That cube that looks like a frame enclosed in the outer cube frame. Then the opposite base of rotation is i. In the illustration above, this peak looks directly at the viewer.
But not third embedded cube with runes (it will perform auxiliary functions).
That rotation of the volume of the three-vector of the outer cube will coincide with the rotation of the enclosed frame.
If you do not take into account the rotation of the inner frame and the direction of its axis of rotation. That conditionally we can assume that 1 is in the bottom vertex of the outer frame. And it is at the top vertex.
p-numbers
This number is named after Wolfgang Pauli.
All the above numbers are scalars, vectors, bivectors, trivectors (pseudoscalars) are called p-numbers. They can be summed up and subtracted among themselves. There are also other algebraic operations, which can be given a geometric interpretation. The resulting number can be called a hypercomplex number.
Complex number
An important property of a trivector is that the tri-vector, when multiplied by itself, is the imaginary unit of the algebra of complex numbers. That is, it specifies a mapping of itself relative to the center of the cube. You can imagine it like this. First we move along the main diagonal to the opposite vertex, which we denote by i. Another such mapping relative to the center reverses the sign and we again find ourselves at the vertex 1, entering it. This operation can be denoted by -1 (minus one).
i2 = -1
Thus, the element of the directed volume formed by the basis elements is identically equal to i (complex number). Thus in the Clifford algebra there exists a subalgebra isomorphic to (analogous) to the algebra of complex numbers whose elements commute (can be multiplied both left and right) with all p-numbers.
Thus, the main diagonal between 1 (Unit) and i (Complex number) forms the algebra of complex numbers.
Quaternion
The sum of a unit with three bivectors (oriented flat elements or pseudovectors) with exponents is isomorphic (similar) to the Quaternion algebra.
An arbitrary quaternion q = a + b i + c j + d k can be represented as a pair of complex numbers in the form q = (a + b i) + (c + d i) j.
It is possible to recalculate the current position of the bivectors i, j, k (i12, j23, k31 bivector) into the rotation angles of the axes of all three rotating cubes.
Inversion of the order of multipliers
If we rearrange the indices in places, then the bivector and the trivector change sign. There is a change in the direction of rotation of the volume of the cube.
The inversion of the direction of the spatial orthes
If you change the sign and direction of each vector, then the sign of all vectors and trivectors changes. So instead of i we get -i.
When the sign changes, the direction of rotation of the unit vectors changes in the negative continuation of the cube (the mirror cube relative to the plane passing through the scalar (unit)).
Since the signs of scalars and bivectors do not change, these elements form an even group. In particular, it is applicable to the description of the magnetic field, since the topology of the magnetic field is even. It is these elements that form the Quaternion group.